《 なるほど数学コラム:高校編 2》 『 微分とは? ~ 曲線から直線へ 』

今回は、イメージしにくい、数Ⅱの『 微分 』の考え方について一緒に考えてみましょう。
数Ⅱの 『 微分 』 の授業が始まり、その導入部分で、学校の数学の先生が、「 定義に従って・・・ 」とか、「 微分係数を求めると・・・ 」,「 導関数が・・・ 」などという言葉をどんどん使って、授業がどんどん進んでいったりします。まるで、外国語を聞かされているようです。
そしてさらに授業が進み、なんだか公式を当てはめさせられて、計算はできるものの、実は自分は何を計算しているのか ( させられているのか ) さっぱりわからない自分がいたりします。
『 微分 』 あるあるです。
みなさんは、いったい何の計算をしているのでしょうか?
微分の定義を見てみましょう。
ウィキペディアでは、このように定義されています。「微分は、ある関数のある点での接線、或いは接平面を考える演算である。数学的に別の言い方をすると、基本的には複雑な関数を線型近似して捉えようとする考え方である」
?????
もうやめます?
やめないでください。
さっきの定義の下線部分をもう一度みてください。その部分を、言葉を補い、かんたんな言葉で言い換えると、「・・・曲線でできている複雑な関数を、直線に直して捉えようとする考え方・・・」ということができます。
そうです。『 曲線から直線へ 』 捉えなおす方法を、みなさんは学習しているのです。
もう少し、イメージを膨らませましょう。
一人の重要人物が登場します。
古代から、微分の考え方につながる計算法(主に面積や体積を求める方法)が考えられてきました。その流れの中で、近代において、万有引力の発見で有名な学者「アイザック・ニュートン」が、『 微分 』の考え方を確立させたとされています。
ニュートンは、物理学や天文学そして数学などでたくさんの功績を残しました。中でも、古典力学の基礎を築いた画期的な著作で、近代科学における最も重要な著作の一つと言われる 『プリンキピア』(あるいは『自然哲学の数学的諸原理』)という本の中で、運動の法則を数学的に論じ、天体の運動や万有引力の法則を扱いました。
その中でニュートンは、当時の数学用語に合わせて微分計算や積分学の手法を使い、天体の軌道、回転流体の表面の形、地球の偏平率、サイクロイド曲線上をすべる錘の動きなど、様々な問題について論じたのです。
いずれも『曲線』,『曲面』が関係する運動ですね。ニュートンは、その『曲線』や『曲面』を詳しく調べることを試み、理論を打ち立てていきました。このことが、『微分』の基礎となっていったのです。
例えば、曲線を詳しく考えるとどうなるでしょうか?
下の図を見てください。y=x²のグラフです。
このグラフの状態を詳しく知ろうとして、マルで囲んだ部分を拡大するとどうなるでしょうか?
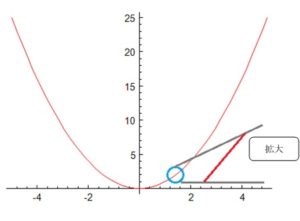
直線に近くなります!
これが、『 微分 』の原理 です!
『ある曲線の区間を極小な部分 ( 限りなく0に近い範囲 ) を切り取ったとき、どんな直線になっているか』を調べることが『 微分 』なんです。
その直線の調べ方は、中学校で調べたやり方と同じです。『どんな傾きの直線になっているか』ということです。それは、『 変化の割合 』という言葉で習ったと思います。
ちょっと思い出してみてください。中学校の時は、「比例」や「一次関数」では、直線を扱っていました。直線だったので、「変化の割合」が いつも一定 だったのを覚えていますか?
でも、三学年になり、「二次関数」を勉強した時、「変化の割合」は一定ではなくなりました。そのときはあまり不思議に思わなかったかもしれません。「そういうものだ」と受け入れていたかもしれませんね。
なんとなく “ピン”ときませんか?
「二次関数」は、曲線 なので、あたえられる区間ごとに「 変化の割合 ( = 傾き ) 」が変わって当然なのです。( ※ 『微分』の勉強を進めてゆくと、一つの曲線を極小な区間で切り取った 変化の割合 ( = 傾き ) は、ある一定の割合で変化する ( もしくは数式で表わすことができる ) ということがわかってきます。 )
そうです。実は、中学校の三年生当時、『微分』という言葉は使っていませんでしたが、『微分』の入り口の勉強をしていたのです。区間が極小ではなかっただけの話です。
まとめてみると、『 微分 』とは、『 いろいろな曲線(関数)の ある点(極小な区間)における、曲線を直線に直してみた時の傾き具合がどうなっているか(一定のどんな関数で「傾き」を導き出せるか)を調べる方法 』ということができます。
どうですか?
イメージわいてきました?
そうすると、この考え方がスーッと腑に落ちると思います。
関数 y=x² の 一般の x の点における傾きを求めます。この点から h だけ離れた点との、2点間における変化の割合は、
と表わすことができます。
2点間のx座標の距離hを限りな0(極小)にすると、この式は 2xとなります。したがって、関数 y=x² の各xに対して、その点における傾きは 2x となります。これが、微分の考え方の基本です。
ここで、y=x² を微分する過程で、xの変化量hを限りなく0(極小)に近づけるという表現をしました。これは、極限の記号 limの下にh→0と書くことで表します。つまり、次のように書き表します。( ※ lim は「リミット」とよみ、極限(limit)を取る記号です。)
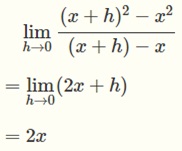
いかがですか?
「 定義に従って・・・ 」とか、「 微分係数を求めると・・・ 」という、学校の先生のフレーズがわかったような気がしませんか?
そうなったらしめたものです!
『 微分 』ワールドへようこそ!
ゆくゆくは、いろいろな関数や曲面の微分も自由自在ですよ!
「そこまでは・・・」って?
大丈夫。
『 微分 』 の世界を心ゆくまで楽しんでください!(笑)