《 なるほど数学コラム:高校編 4》 『 格子点の問題 ~ 長さのちがう団子がならぶ 』

今回は、「数列」 の応用問題
『 格子点 』
についてです。
この 『 格子点 』 の問題というのは、
「 座標平面上の決められた領域 ( ※ 通常は、関数とx軸やy軸で囲まれた領域が設定されます。) の中で、『 x座標、y座標とも整数である点 』がいくつあるか 」
を、 数列の計算を使いつつ求める 問題です。
そしてこの問題、問題集によっては、☆が4つほどついていて ( レベル4 [最難問クラス] ) 、なおかつ、解説がややこしい。
「 もういいや 」
なんて思いがちです。
いやいや、あきらめないでください。
イメージがつかめれば、けっこう解けてしまったりしますよ。
「どんなイメージですか?」 って?
今日のタイトルの
『 長さのちがう団子がならぶ 』
です。
こんな感じです。
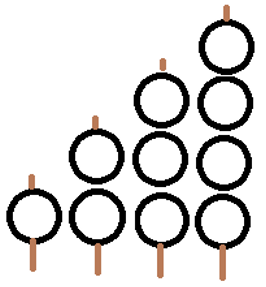
じゃあ、じっさいにどうするか。
基本パターンを考えてみましょう。
よくあるパターンは、こんな問題です。
曲線 y = 2x³ – 15x² + 24x + 4 ( 0≦x≦N ) と x軸 および x=N で
囲まれた領域(境界を含む)にある格子点の個数を求めよ。
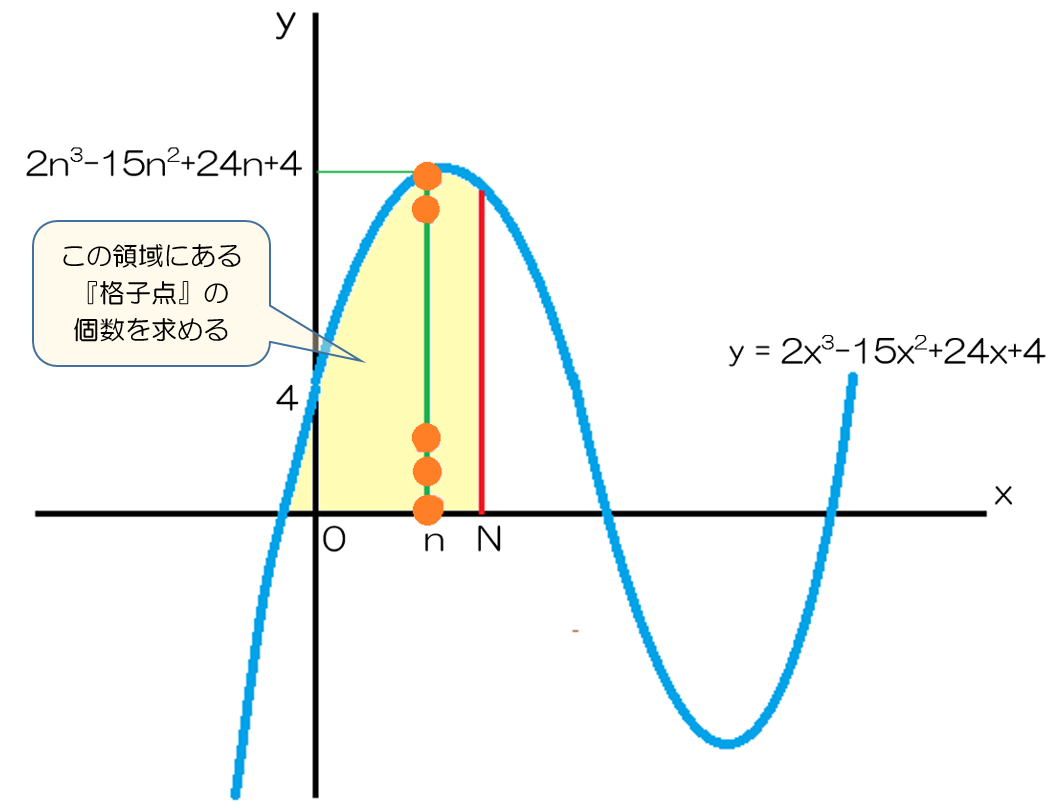
やめちゃいます?
やめないでください。
まず、問題で与えられている、0からNまでの間で、
ある一般的な長さの “ クシについている団子の数 ”
を求めておきます。
ここでは、
x = n という クシについている団子の数
を数えると思ってください。
x = n の時の yの値は、2n³ – 15n² + 24n + 4 になりますね。
そうすると、x = n の団子は、境界線上も含むので、
(n , 0), (n , 1) , (n , 2) , ・・・・・・, (n , 2n³-15n²+24n+4)
までの団子 ( = 格子点 ) があることになります。
そうすると
x = n上の格子点の個数は、x軸上にある、0番目の点も数えますので、
2n³ -15n² + 24n + 4 + 1 個
となります。(←ここポイントです。)
計算すると
2n³ -15n² + 24n + 5 個
ですね。
こんなイメージです。

x = n というクシについている団子の数は、 2n³ -15n² + 24n + 5 個 です。
このクシが、
x = 0 から x = N まで並んでいる
と思ってください。
それをどうやって計算すればよいかというと、
『 ひとクシあたり 2n³-15n²+24n+5 個 ついている団子のクシを、0番目からN番目までならべて、全部足し合わせる 』
と考えるので、
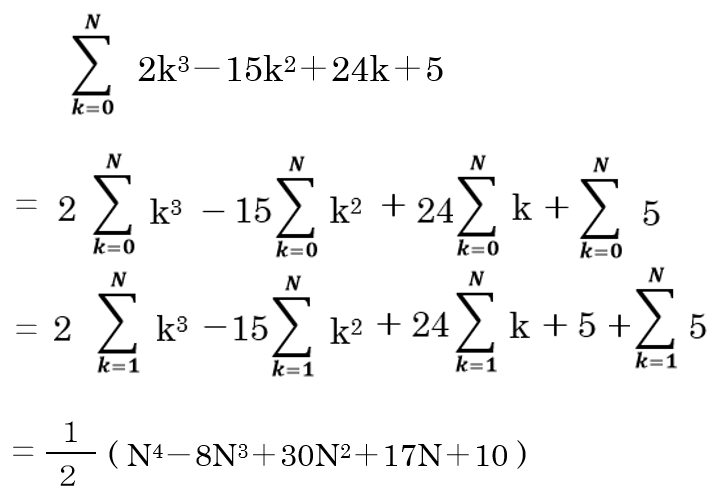
となります。
詳しい計算法については、「なるほど数学コラム:高校編 No.1」 ( ← リンクです。クリックするとそのページに移ります。) をみてください。
というわけで、
この問題
「曲線 y = 2x³-15x²+24x+4 ( 0≦x≦N )と x軸 および x=N で囲まれた領域(境界を含む)にある格子点の個数を求めよ。」
の 答は、

となります。
ちなみにこの答えに、N = 0 をあてはめてみると、5個 になります。
グラフで確かめてみると、この関数(y = 2x³-15x²+24x+4)は、y軸上の4が切片になるため、N = 0 (すなわち x = 0 = y軸上)にある格子点の数が 『5個』 になっていて、答の式で導き出された個数と合っていることがわかります。
格子点の問題の解き方をまとめてみると、
1.問題で与えられた関数にx = n と代入し、その答えに、x軸上にある0番目の分として 『 1 』を足し合わせ、『ひとクシあたりの格子点(団子)の個数の式』を求める。
2.ひとクシあたりの格子点(団子)の個数の式を、与えられた区間分 ( 0番目からN番目の場合がほとんど )ならべるイメージで、Σ計算で全部足し合わせる。
- 問題によっては、クシの向きを横向きで考えたほうがいい場合もあります。
この2ステップで、“ ☆4つ ”の格子点問題も克服です!
『 長さのちがう団子がならぶ 』
イメージで、格子点の問題、どんどん解いちゃってください !!!!!!!