今回は、間違えやすい数列の計算について一緒に考えてみましょう。

キーワードは、『実体のある“０(ゼロ)”』です。別名『０番線のメソッド(方法)』です。

どんなものか、みてみましょう。

間違えやすいΣの計算問題の一例をあげます。

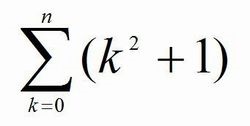
「こんなの簡単ですよ！」って言って、こんな計算をしないでくださいね。
これは間違いです。

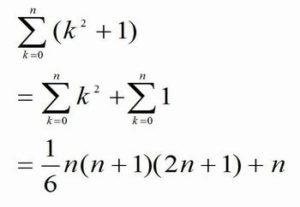
この計算、左半分は合っています。この公式を当てはめようとしていると思います。

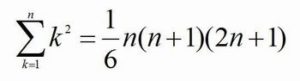
この公式の左辺は、「kの２乗で表される式にk=1,2,3,…,nを代入していき、それらを全て足し合わせる」という意味です。これをΣを使わずに書けば、次のようになります。

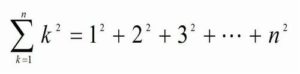
同様に、k=0で始まる場合もΣを使わずに書いてみます。0の2乗は0なので無視すると、k=0で始まる式は、k=1で始まる式とイコールの関係になります。

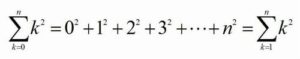
したがって、間違いの例の1/6の項は正しかったと言えます。とはいえ、これは、たまたま正しかっただけということもできます。

次に、間違いの例の右半分です。これは、以下の公式を当てはめてしまったといえます。

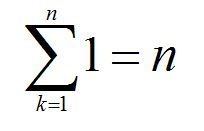
この公式の左辺は、「1番目からn番目まで1で表される数列をすべて足し合わせる」という意味です。つまり、1が全部でn個あるので、その総和がnなのです。

この公式のk=1がk=0に変わったらどうでしょうか？

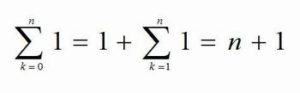
k=1で始まる公式に『 0番目の1 』が加わるので、上のように書き換えました。この結果から、k=0で始まる式と、k=1で始まる式とはイコールの関係にはならないことが分かります。

この説明で、納得できない生徒さんが出てきます。

 

 

「 『 0番目の1 』って なに ??????!!!!!!!!!! 」
「 『 ０ 』ってことは、なにもないことじゃないの ?????? 」

「 なのに、『 ０番目 』に『 １ 』があるってどういうこと ?????? 」

 

言いたいことはわかりますよ。

 

 

ここで登場するのが、『実体のある“０(ゼロ)”』という概念です。

 

要は、「 『 ０番目 』に『 １ 』という『実体』がある 」という考え方です。

 

実際に、この世の中には、「 『実体』がある『 ０ 』 」というものが存在します。

 

一例をあげてみましょう。

 

みなさんは、電車に乗ったことがありますか？
電車に乗るときには、駅のホームから電車に乗ります。
駅のホームには、番号がふられています。
普通は、１番線，２番線 ･･･というふうになっています。
これは、１番目のホーム，２番目のホーム，･･･という意味です。

 

 

しかし、駅のホームを作る都合上、１番線・２番線･･･の前に番号をふる必要が生じたホームが存在します。

 

そのホームには、 『 ０番線 』 という番号がふられます。
これは、 『 ０番目のホーム 』 という意味になります。
これはすなわち、「 『 ０番目 』に『 ホーム 』という『実体』がある 」ということになります。

 

納得できたら、正解を見てみましょう。

こうなります。

『実体のある“０(ゼロ)”』 ，『 0番目の1 』 という考え方をしっかりと身に付けて、正確な k=0 の Σ計算をしていきましょう。