《 なるほど物理コラム:2 》 『 “ 電場 ” とは ー その2 』

前回のコラムでは、
「 電場とは何か 」
ということ、そのイメージとともに考えました。
今回は、
「 電場の大きさ 」
について考えてみましょう。
さっそくですが、池に石を投げ入れたところをイメージしてみてください。

石を投げ入れた中心にははっきりとした波が立ち、中心から遠くなるにつれて、
波が小さくなっていきますね。
本来は「波動」の分野になるのでもっと様々なことを考えなければならないのですが、
今回は、あくまで「イメージ」として考えると、
「 中心から離れてゆくにしたがって、中心からの影響力が弱まってゆく (波が小さくなってゆく) 」
ということをイメージできると思います。
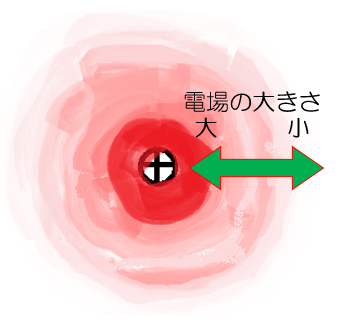
これと似たようなイメージで、改めて電場について考えてみると、
「 電荷が置かれている中心から離れてゆくに従って、
電場の大きさが小さくなってゆく」
と考えることができます。
( ※その逆に 『 電荷が置かれている中心に近づいてゆくに従って、
電場の大きさが大きくなってゆく 』 とも考えることができます。)
もう少し、考えを深めてみましょう。
電荷の持つ電気力を『 静電気力 』といいましたね。
そして静電気力には、正(プラス;+) と 負(マイナス;-) がありましたね。
また、あるところに二つの電荷があったと仮定すると、
その二つの電荷の静電気力の差を
『 電位差 』
といいました。
このことと、
『 電場の大きさ 』
を結び付けて考えてみましょう。
先ほど説明した、
『 静電気力 』 と 『 電位差 』
そして
『 電場の大きさ 』
を合わせたグラフや図は以下のようになります。

中学校の理科の 「 気象 」 の学習の時に、
「 等圧線 」;「 高気圧 」・「 低気圧 」
について学んだと思います。
その時に、
「 等圧線の間隔が短い方が風力が大きく、
等圧線の間隔が広い方が風力が小さい 」
と、習ったことと思います。
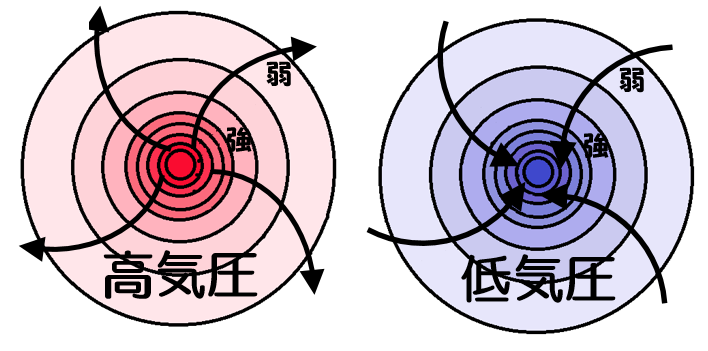
電場も同様に、
「等電位線の間隔が狭い方が電場の大きさは大きく(強く)、
等電位線の間隔が広い方が電場の大きさは小さい(弱い)」
とみなします。
次に、「地理」の「地形図」の話も思い出してみましょう。
地形図では、同じ高さを結ぶ「等高線」というものがありましたが、
「 地形の傾きが急になっているところは、「等高線」の間隔が狭く、
傾きが緩やかになっているところは、「等高線」の間隔が広く」
と なっていました。
こんな感じです。
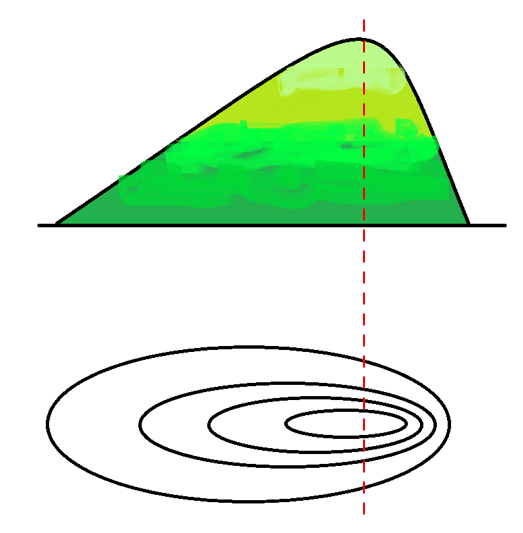
傾きが急なところは、頂上に近く、
傾きが緩やかなところは、頂上から離れていますね。
電場のグラフも同様に考え、
傾きが急なところは、
電荷が置かれたところに近いので、電場の大きさは大きく(強く)なり、
傾きが緩やかなところは、
電荷が置かれたところから離れるので、電場の大きさは小さく(弱く)なるのです。
そういった観点で見ると、先ほどの電場に関する図がわかりやすくなります。

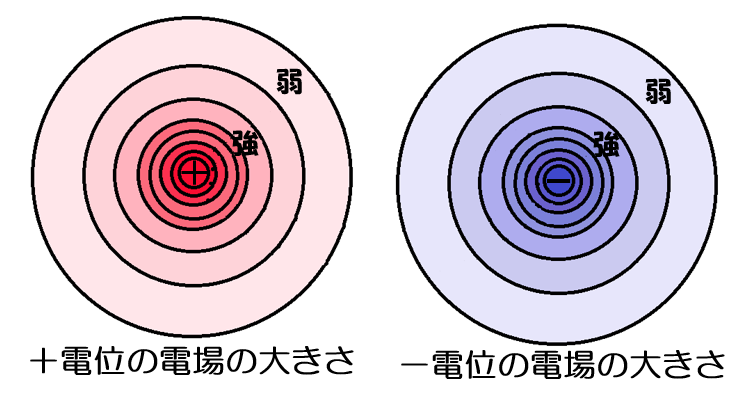
+の電荷,-の電荷をそれぞれ置くと、電位差が生じます。
( ※電気力線の向き:+ → - )
+の電荷,-の電荷 それぞれの周りに『電場』が発生します。
『電場』は、それぞれの電荷の近くでは大きく、離れると小さく
なります。
最後にもう一点。
『 電場 』は、『 空間 』でした。
『 空間 』は、たて・よこ・高さ がある、いわゆる3次元の空間ですね。
3次元の空間での大きさを比べるときには、どんな考え方を使えばよかった
でしょうか?
『 向きと大きさ 』が関係する量ですね。
『 向きと大きさ 』が関係する量といえば、『 ベクトル 』※ ですね。
( ※ 『 ベクトル 』に関しては、
「 《 なるほど数学コラム:高校編 》 No.8『 “ ベクトル ” とは?』」
[ ← リンクです ] をご覧ください。)
そのため、『 電場 』は、『 ベクトル 』の計算で考えるのです。
どうですか?『 電場 』のイメージがわきましたか?
イメージが持てれば、あとは演習あるのみです。
大丈夫。できるようになりますよ。
『 電場 』の世界へようこそ!