《 なるほど数学コラム:高校編 8》 『 “ ベクトル ” とは? 』

たいてい高校2年生※の 『 数B 』 の授業で、『 ベクトル 』 という単元の学習をします。
【 ※中高一貫校や進学校の一部では、もっと早い時期に学習する場合があります。 】
こんな感じのモノの演算の勉強です。

「 矢印の勉強??? 」
いやいや違います。
『 ベクトル(vector) 』 というのは、語源はラテン語の「運ぶ者」で、
「方向・進路・方向量」といった意味の言葉です。
数学においては、『 向きと大きさを持つ量 』 と 定義 されます。
また『 ベクトル 』は、矢印のように見える有向線分 で表され、
その 矢印の向き が ベクトルの向き を意味し、
長さ が ベクトルの大きさ を意味するものとなっています。
ちなみに、『 物理 』 の 「(物体の)運動」 や 「電気・磁気」 などの単元でも
『 ベクトル 』 が登場します。
平面や空間上における力や速度などは、ベクトルで表されるからです。
話を数学に戻します。
『 ベクトル 』 の単元の授業が始まると、ほどなくして、
ベクトルの加法や減法などの計算を学んでゆく流れになりますが、
計算法が独特なため、生徒さんによっては、ふと、
「 自分はいったいなにをしている ( させられている ) のだろう? 」
と思い、混乱してしまうことがあります。
『 ベクトル 』 に対するイメージをきちんと持てているかいないかで
「解ける・解けない」,「覚えられる・覚えられない」が変わってくるため、
そこをきちんと押さえることにしましょう。
まず、 これまでの数学・算数とは違う という考えを持ちましょう。
例をあげます。 加法(足し算)で考えてみましょう。
まず、これまでの数学(算数)の世界で当たり前だった 加法(足し算) のパターンです。
問題. りんごを一つ![]() 木から採りました。
木から採りました。
さらにもう一つ 木から採りました。
木から採りました。
合わせていくつ採ったでしょう?
「 そーんなの、かんたんじゃないですかー !!!!!!!!!!!!! 」
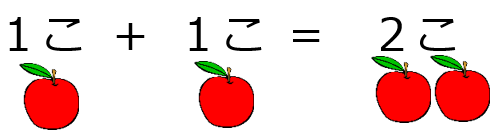
「 2こにきまってるじゃないですかー!!!!!!! 」
まあ、そうですよね。
これが、今まで当たり前だった 加法(足し算) です。
では、ベクトル での 加法(足し算) はどうなるでしょうか?
問題. 家から![]() 1km南に進みました。
1km南に進みました。
さらにそこから西にもう1km進み、コンビニに 行きました。
行きました。
家からコンビにまではどれくらいはなれているでしょうか?
これは、単純に

とはいきませんね。
こんな感じになります。
三平方の定理を使って
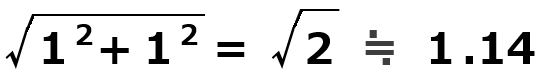
となるので、
「自宅から見て、南西に約 1.14 km離れた場所にある」 が
答えとなります。
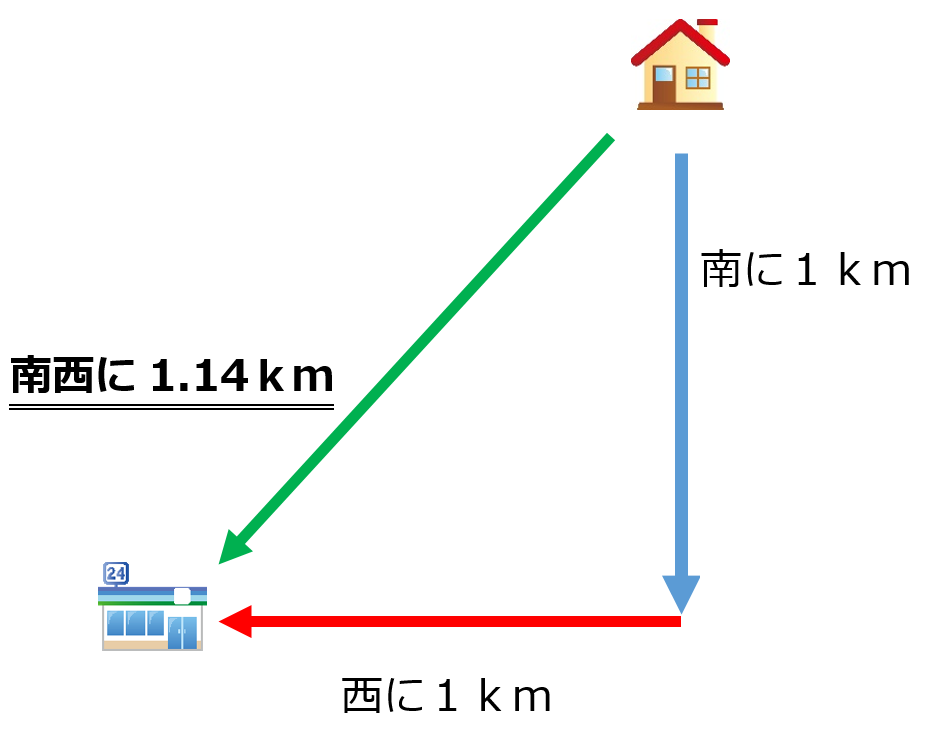
これが、ベクトルの加法(足し算)の考え方です。
このように、「 大きさ 」に加えて「 向き 」も持った量を使うことで
2次元平面や3次元空間上のものごとを数式に取り入れて考えることが可能になるのです。
だんだんなれてきますが、とても便利なんですよ!
それでは、新しい数学の世界 『 ベクトル 』 を存分に楽しんでください!